Global maxima in fitness landscapes

This blog post states a problem, does not provide any solutions. This is a high form of whining.
Background
Here I present Kauffman’s NK model. Let agents face a complex decision x, i.e. a decision that consists of N interacting sub-decisions: x = (x1,x2,…,xN). For simplicity, assume that decisions are binary (either 0 or 1). Let every sub-decision be “coupled” with K other decisions, i.e. the performance fi (xi) = fi (xi,xi1, …, xiK). Finally, for simplicity, assume that the performances f(.) are uniform random.
Problem statement
There are two ways to model a search process — (a) generate the reference landscape of size (N x 21+K) and calculate values according to it, and (b) generate performance values on-the-fly. The advantage of the former is that you can always know what the global maximum of the landscape is, and you can normalize your results accordingly. The disadvantage is that to store landsape for N = 28 and K = 27 you need 56 GB of RAM and lots of CPU time. Don’t even dream of parallelizing or running 100 repetitions.
We have the simplest model you can imagine and can’t even get to 30 decisions — if you allocate 4 decisions to 7 people… ummm, well you can’t do that apparently.
Why (b) won’t work
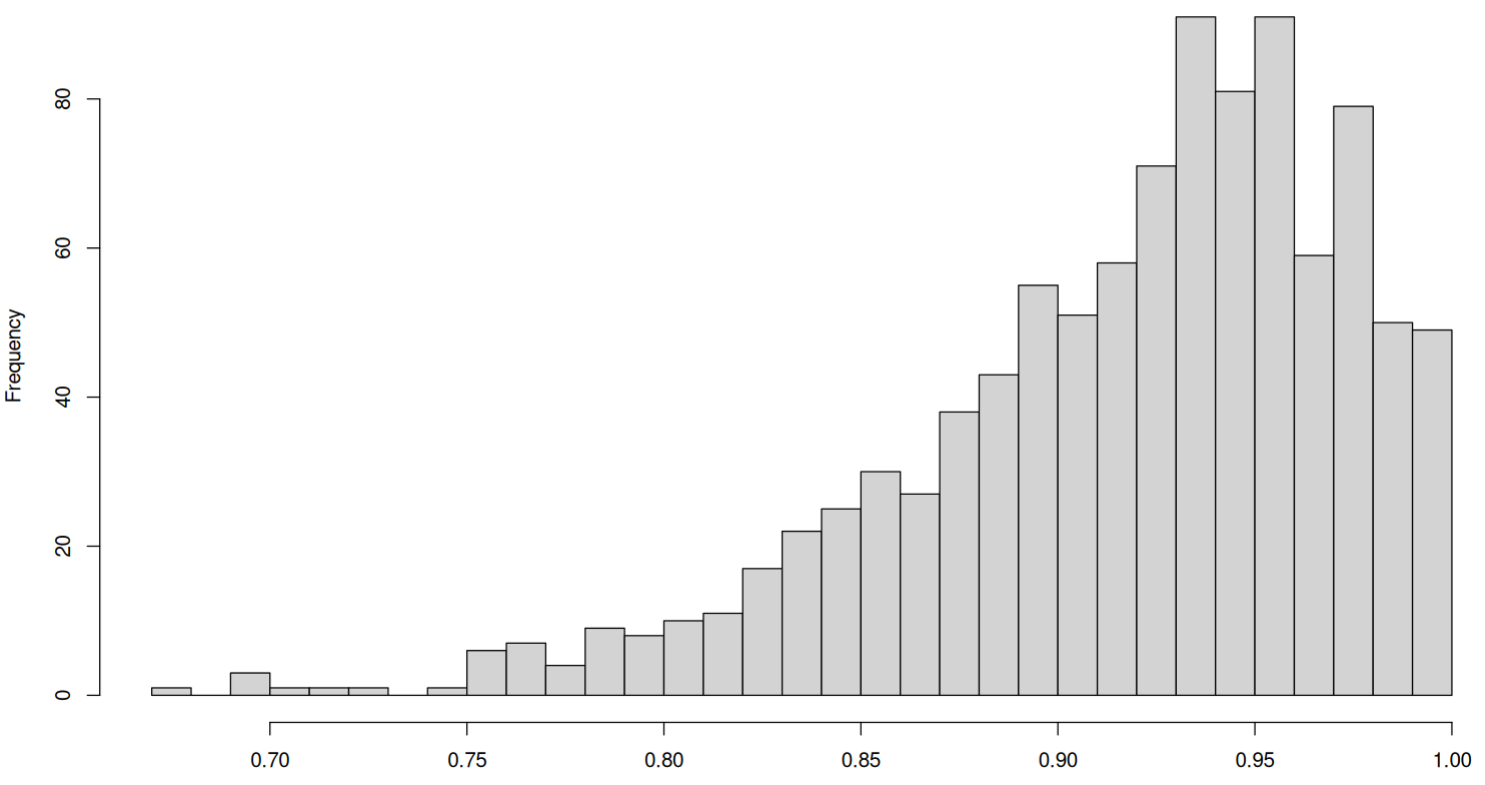
OK, so let’s say we have decided to generate values on the fly and estimate the global maximum. What is wrong with that? The problem is that the higher the value of K, the closer is the maximum to 1 (tail probabilities), but at the same time, the higher is the N, the lower is the maximum of a sum (multiple columns can’t be high at the same time). The answer probably lies somewhere in the ratio K/N, like it was mentioned in Kauffman’s 1991 avalanches paper. But I can’t tell, to be honest.
Conclusion
Life is difficult.
Update I have made some sensitivities on K/N, here are the results:
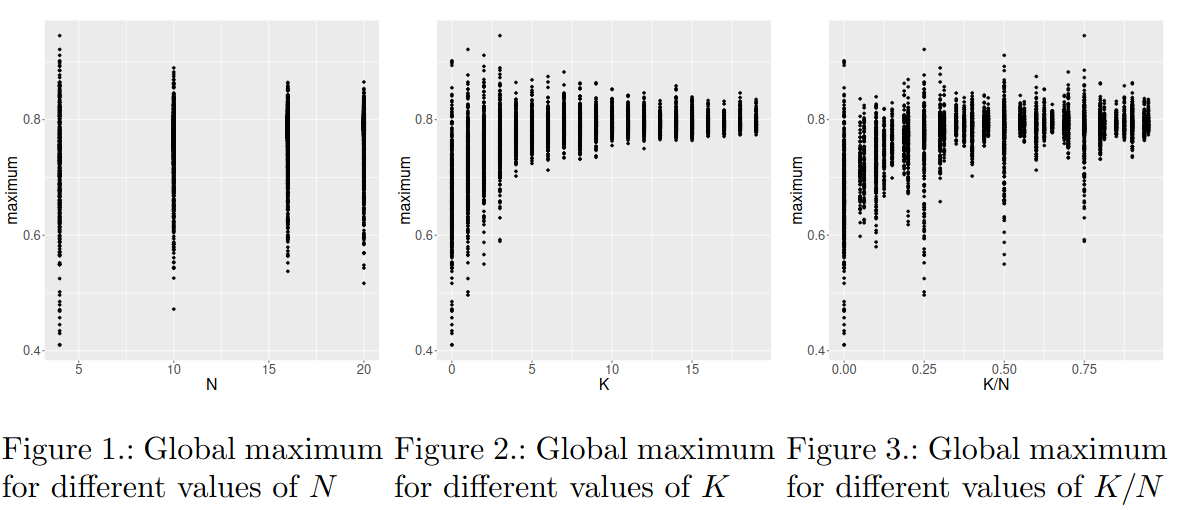
So, … kinda proves my point: there is a pattern, but too risky to straight out assume. ikr: if I solved this, then I would solve P vs. NP problem.
A new conclusion: pick your battles!